Projektbeschreibung

Werden Strukturen mit der FE Methode auf Stabilität  untersucht, so wird zumeist nach Verzweigungs- und Durchschlagspunkten gesucht. Hierbei werden bei statischen Untersuchungen  Pfadverfolgungsalgorithmen eingesetzt, um als Ergebnis eine Lastverformungskurve zu erhalten. Die Richtigkeit und Eindeutigkeit  der erhaltenen Kurve ist aber oft problematisch, z.B. bei Tragwerken mit mehreren Verzweigungspunkten und Pfaden oder Problemen mit Kontakt. Ausserdem ist für die praktische Bemessung nicht nur die Gleichgewichtslage (GGL) an sich, sondern vielmehr ihre Realisierbarkeit von Interesse. Besitzt ein System mehrere GGLn bei einem Lastniveau, so kann es durch Zuführen von Energie, z.B. kinetischer Störung, von einer stabilen GGL in eine andere überführt, oder zu freien Bewegung angeregt werden. In Realität können diese Störungen beispielsweise Windstöße oder im Extremfall ein Aufprall sein (z.B. KFZ, Bahn, Flugzeug). Der Kehrwert der minimalen kinetischen Energie, die hierzu notwendig ist, wird als Sensitivität definiert S=1/W_kin,min. Folgende Rechenschritte zu Ermittlung der Sensitivität werden durchgeführt:

1. Statische Berechnung bis zur GGL, die auf Sensitivität untersucht werden soll
2. Zuführen von Störungsenergie, z.B. Definition von Geschwindigkeitsanfangsbedingungen (Dirac Stoß)
3. Transiente Berechnung zur Ermittlung der gestörten Bewegung
4. Betrachtung der gestörten Bewegung: 
   • Führt die Struktur eine Schwingung um die Ausgangs-GGL aus, so kann die Störenergie erhöht werden.
   • Verläßt die Struktur den Einzugsbereich der Ausgangs-GGL, d.h liegt Bewegung zu einer anderen stabilen GGL oder eine freie Bewegung mit unbegrenzt anwachsenden Verschiebungen vor, so muß die Störenergie reduziert werden.

Beispielsweise kann für einen axialbelasteten Zylinder die in Bild 1 dargestellte Lastverformungskurve ermittelt werden. Die stabilen Gleichgewichtlagen sind mit grüner und die instabilen mit roter Farbe dargestellt. Wie man sieht, besitzt der Zylinder im Lastbereich bis 50 kN nur eine stabile GGL. In diesem Lastbereich kann der Struktur beliebige Störenergie zugeführt werden, ohne ein Versagen auszulösen (elastisches Materialverhalten vorausgesetzt), die Struktur wird lediglich zu Schwingungen um die GGL angeregt. Oberhalb der Last von 50 kN besitzt der Zylinder eine stabile und eine instabile GGL. Hier wird der Zylinder nur für genügend kleine Störenergien Schwingungen um die Ausgangs-GGL ausführen. Ist die Störenergie groß genug, so verläßt der Zylinder den Einzugsbereich der Ausgangs-GGL und bildet Beulen (siehe Bild 2), was zum Versagen führt.

Interessant sind in diesem Zusammenhang folgende Fragen:

1. Welche Geschwindigkeitsverteilung bei der Störung führt zu höchsten Sensitivität?
2. Wie kann die gestörte Bewegung analysiert werden, um effizient eine Entscheidung über die Art der Bewegung treffen zu können?

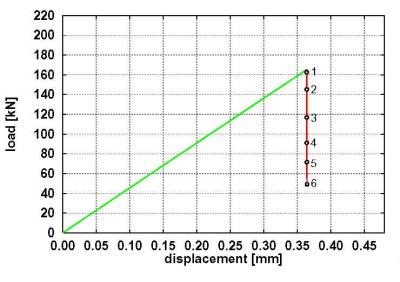Bild 1: System und Lastverformungskurve

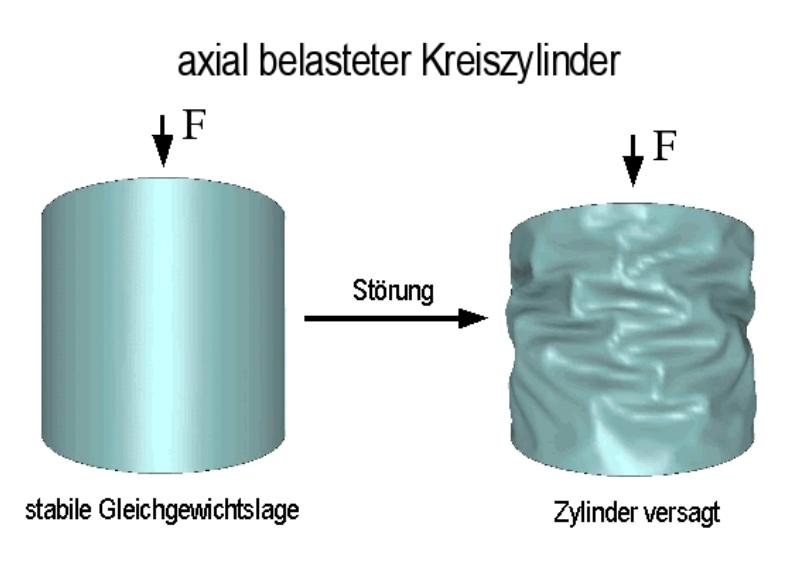Bild 2: Kreiszylinder in einer stabilen Gleichgewichtslage im Vorbeulbereich (links) und die Beulenbildung nach Zuführen kinetischer Störung (rechts).