 The most powerful approach in the computational contact mechanics is to work in accordance with the geometry of contact bodies and construct all computational algorithms in a covariant form. This combination forms a geometrically exact theory of contact interaction.
The most powerful approach in the computational contact mechanics is to work in accordance with the geometry of contact bodies and construct all computational algorithms in a covariant form. This combination forms a geometrically exact theory of contact interaction.
The main basis of the theory is that the Closest Point Projection (CPP) procedure corresponding to a certain geometrical feature gives rise to a special, in general, curvilinear 3D coordinate system. This coordinate system is attached to a geometrical feature and its convective coordinates are directly used for further definition of the contact measures. Thus, all possible shown contact pairs can be described in the corresponding local coordinate system. The existence requirement for the solution of the generalized CPP procedure leads to the transformation rule between types of contact pairs according to which the corresponding coordinate system is chosen. Thus, all contact pairs such as Point-To-Point, Point-To-Line, Surface-To-Surface, Line-To-Surface, Line-To-Line can be uniquely described in most situations in a general manner.
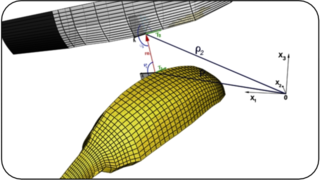
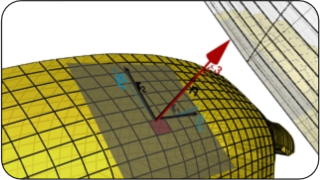
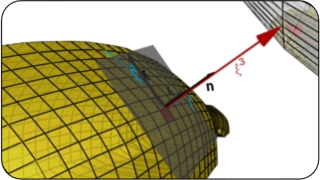 A Surface-To-Surface contact pair is described via the well known "master-slave'' contact algorithm based on the CPP procedure onto a surface. This projection allows to define a coordinate system as follows:
A Surface-To-Surface contact pair is described via the well known "master-slave'' contact algorithm based on the CPP procedure onto a surface. This projection allows to define a coordinate system as follows:
r(ξ¹, ξ², ξ³) = ρ(ξ¹, ξ²) + ξ³ n(ξ¹, ξ²)
where ξ¹, ξ² are measures of the tangential interaction and ξ³ is a measure of the normal interaction
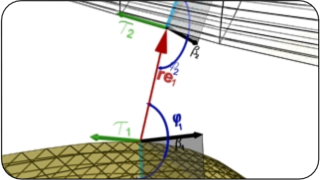
 Consideration of existence of the CPP procedure for edges allows to define the Point-To-Line (PTL) contact algorithm used for the Point-To-Line contact pair directly as well as for the Line-To-Surface contact pair. The local coordinate system is constructed as follows:
Consideration of existence of the CPP procedure for edges allows to define the Point-To-Line (PTL) contact algorithm used for the Point-To-Line contact pair directly as well as for the Line-To-Surface contact pair. The local coordinate system is constructed as follows:
r(s, r, φ) = ρ (s) + r e(s, φ); e = ν cos φ + β sin φ
The vector r is describing a "slave'' point from the surface. The convective coordinates are used as measures: r - for normal interaction; s - for tangential interaction; φ - for rotational (torsional) interaction.
The Line-To-Surface contact pair, however, can be described in a dual fashion via the Surface-To-Surface contact algorithm if we consider a "slave'' point on the edge and project it onto the "master'' surface.
 The Point-To-Point contact pair is described then in a coordinate system standard for rigid body rotation problems (e.g. via the Euler angles), however, in contact situations it is a very rare case, and in computations it is rather improbable unless specially treated, and therefore, it would fall into other contact pair types.
The Point-To-Point contact pair is described then in a coordinate system standard for rigid body rotation problems (e.g. via the Euler angles), however, in contact situations it is a very rare case, and in computations it is rather improbable unless specially treated, and therefore, it would fall into other contact pair types.
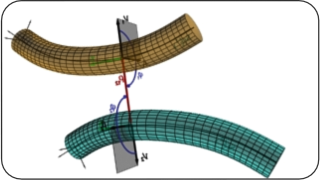
 The Curve-To-Curve (CTC) contact pair requires the projection on both curves, therefore, there is no classical "master'' and "slave'' parts and both curves are equivalent. For the description both coordinate systems assigned to each contacting i-th curve are used:
The Curve-To-Curve (CTC) contact pair requires the projection on both curves, therefore, there is no classical "master'' and "slave'' parts and both curves are equivalent. For the description both coordinate systems assigned to each contacting i-th curve are used:
ρ2(s1, r, φ1) = ρ1(s1) + r e1(s1, φ1); e1 = ν1 cos φ1 + β1 sin φ1
The vector ρ2 is a vector describing a contact point of the second curve, ρ1(s1) is a parameterization of the first curve; a unit vector describing the shortest distance e1 is written via the unit normal ν1 and bi-normal β1 of the first curve. The given equation describes the motion of the second contact point in the coordinate system attached to the first curve.
The description is symmetric with respect to the choice of the curve 1 ? 2. Convective coordinates are used as measures:
r - is mutual for both curve and a measure for normal interaction; si - for tangential interaction and φi - for rotational interaction for the i-th curve.
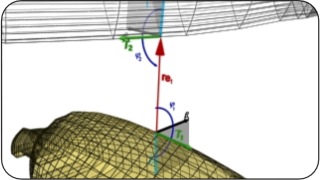 In many cases (STS, PTL, CTC etc.) after the finite element discretization it is necessary to develop a special algorithm to transfer history variables between element boundaries.
In many cases (STS, PTL, CTC etc.) after the finite element discretization it is necessary to develop a special algorithm to transfer history variables between element boundaries.
 The Curve-To-Curve contact algorithm is applied directly for the beam-to-beam contact. In this case constitutive relations are formulated with regards to a cross section, defined in the plane (ν - β) orthogonal to the tangent vector τ. Two tangent forces T1 and T2 acting along tangent vectors allows to describe an anisotropic tangential interaction between beams.
The Curve-To-Curve contact algorithm is applied directly for the beam-to-beam contact. In this case constitutive relations are formulated with regards to a cross section, defined in the plane (ν - β) orthogonal to the tangent vector τ. Two tangent forces T1 and T2 acting along tangent vectors allows to describe an anisotropic tangential interaction between beams.
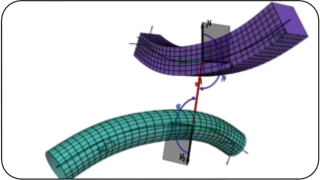 Not only circular cross sections are possible, any arbitrary cross section can be supplied in the plane(ν - β) , however, the definition of the measure for normal interaction is then difficult.
Not only circular cross sections are possible, any arbitrary cross section can be supplied in the plane(ν - β) , however, the definition of the measure for normal interaction is then difficult.
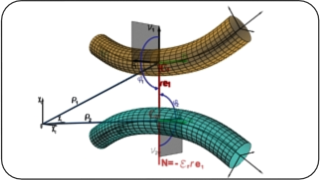 Mutual normal force N is acting along the shortest distance vector e
Mutual normal force N is acting along the shortest distance vector e
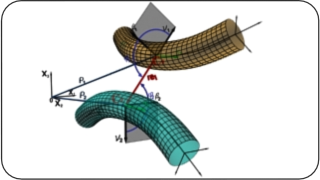 A new achievement of the theory for Curve-To-Curve contact is the possibility to describe rotational (torsional) interaction given by the moment M corresponding to the convective coordinate φ
A new achievement of the theory for Curve-To-Curve contact is the possibility to describe rotational (torsional) interaction given by the moment M corresponding to the convective coordinate φ
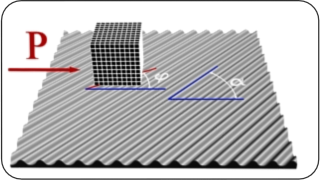 The geometrically exact theory for contact interaction allows a systematic generalization of a contact interface law from the Coulomb friction law into the anisotropic region in a covariant form including various known visco-elasto-plastic mechanical models. Thus, the developed coupled anisotropic adhesion-friction model can successfully describe a set of trajectories of a block on a rubber mat with a periodical wavy profile. The new frictional force is given by the formula:
The geometrically exact theory for contact interaction allows a systematic generalization of a contact interface law from the Coulomb friction law into the anisotropic region in a covariant form including various known visco-elasto-plastic mechanical models. Thus, the developed coupled anisotropic adhesion-friction model can successfully describe a set of trajectories of a block on a rubber mat with a periodical wavy profile. The new frictional force is given by the formula:
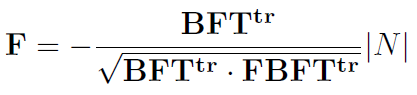
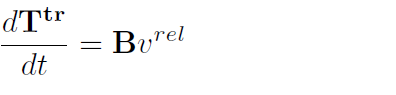
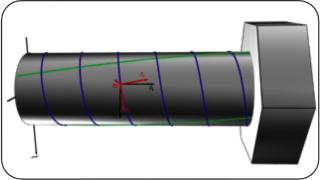 The theory of generalized anisotropic adhesion-friction gives the homogenized model for contact interfaces. Thus, the application of the spiral orthotropy on a cylindrical surface allows to simulate the kinematics of the bolt connection on arbitrary rough mesh.
The theory of generalized anisotropic adhesion-friction gives the homogenized model for contact interfaces. Thus, the application of the spiral orthotropy on a cylindrical surface allows to simulate the kinematics of the bolt connection on arbitrary rough mesh.
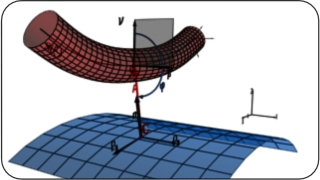 A special algorithm is developed for a contact between deformable curve and a rigid surface (CTRS). It is bades on combination of CTC and Segment-To-Analytial Surface algorithm (STAS).
A special algorithm is developed for a contact between deformable curve and a rigid surface (CTRS). It is bades on combination of CTC and Segment-To-Analytial Surface algorithm (STAS).
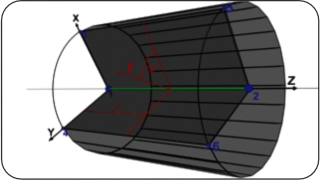 A special Solid-Beam finite element with elliptical cross-section and anisotropy inherited with elliptical coordinate system is developed for the ropes and cables.
A special Solid-Beam finite element with elliptical cross-section and anisotropy inherited with elliptical coordinate system is developed for the ropes and cables.
