Project description

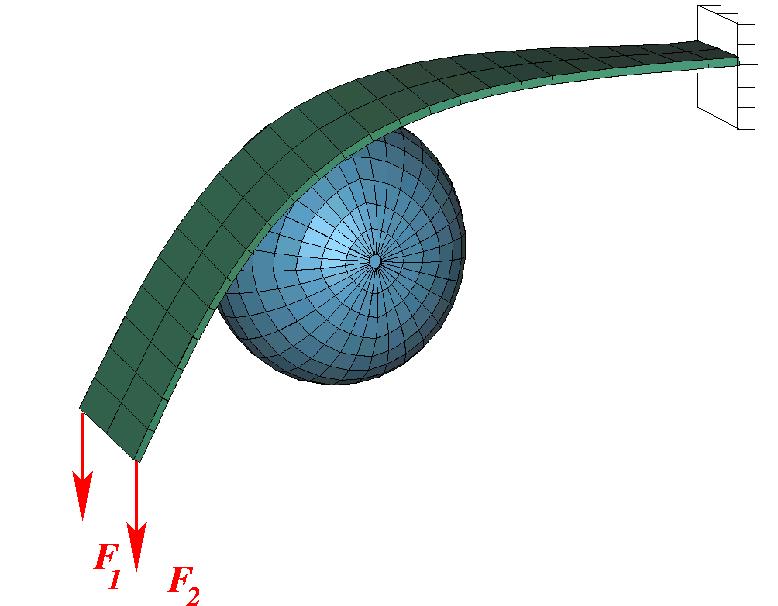
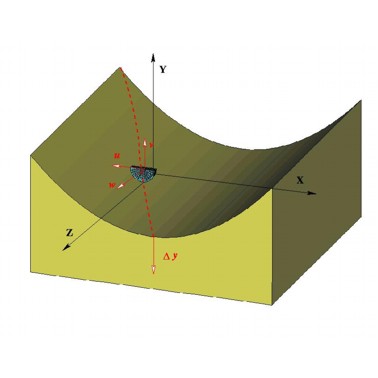
Contact problems are important in engineering practice when the interaction of two and more bodies is considered. This leads to the formulation of contact conditions on the unknown contact surfaces, which makes the problem nonlinear. A great variety of methods is available to solve the problem numerically. These are e.g. the direct solution of the variational inequalities by nonlinear programming, the Lagrangian multiplier method, the penalty method and the augmented Lagrangian method. Further definitions are necessary to define the penetration of the two surfaces into each other. For this the ''master-slave'' concept, based on the definition of penetration of a ''slave'' point S, defined on the so-called slave surface, into the master contact surface, defined via the surface normal pointing towards the penetrator, was found to be a very robust and general technique to define contact. The penetration is then used to construct a contact functional, and therefore also a constitutive model for contact forces. The functional, defined over the a-priori unknown contact surface, is a nonlinear function of the current geometry. Therefore, the whole problem requires an iterative solution, e.g. by a Newton iterative scheme. The latter requires the linearization of the contact functional. Such a procedure is often described in a global reference coordinate system. The core of the covariant description, chosen because of its mathematical elegance, is to describe the contact conditions in a specially defined spatial local coordinate system, which is in general identical to a coordinate system selected for the well-known closest point procedure, see Fig.1. Namely, the surface coordinate system 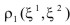,  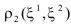leads directly to a spatial coordinate system, defined at the contact point C.

Thus, any spatial vector in space can be defined as ,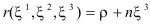

where the third coordinate is the value of a penetration. The base vectors of the system are given as

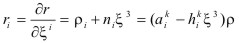
where 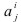 are components of the metric tensor,  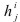are components of the surface curvature tensor. Since contact is an interaction between surfaces each necessary equation especially for the linearization will be considered on the tangent plane, i.e. at 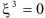. The differential operations are considered in the covariant form. This allows to obtain a description which is applicable to any approximation of the contact surface, i.e. in the covariant form. A formulation of the evolution equations in the covariant form allows to generalize the contact conditions e.g. to include various contact interface laws. The numerical examples show the robustness of the current description.

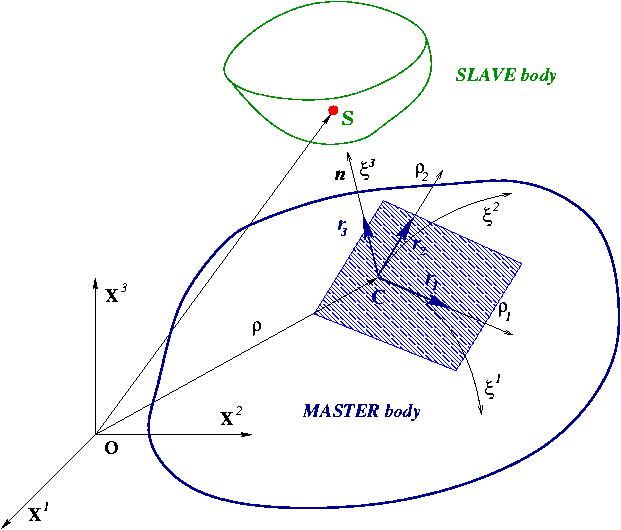
Figure 1: Introduction of the local surface coordinate system

2. Frictionless contact

2.1 Bending of a plate over a sphere. Large deflections and contact

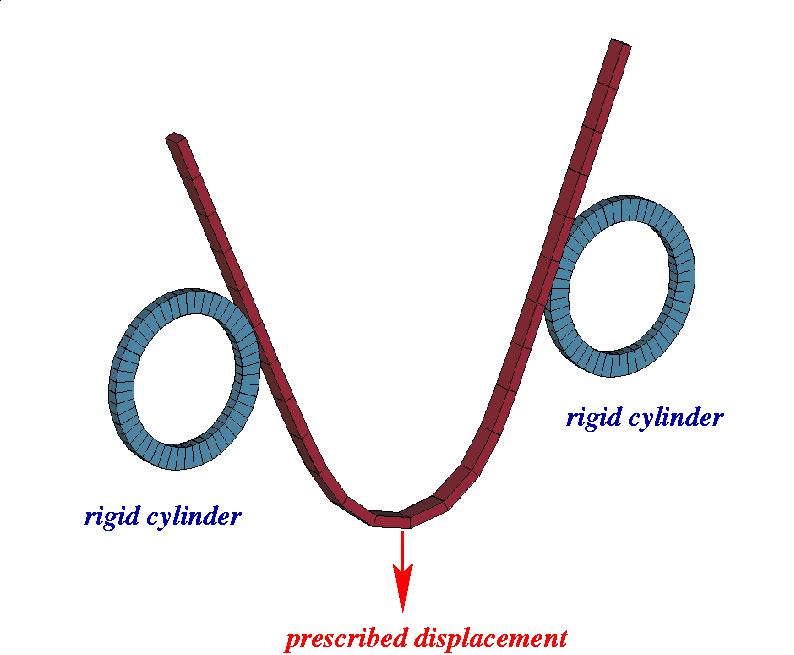
2.2 Large sliding between cylinders

3. Frictional contact

3.1 Spiral motion of a semi-cylinder on a rigid parabolic cylinder

3.2 Deep drawing problem